Overview
About
GCTB is a software tool that comprises a family of Bayesian linear mixed models for complex trait analyses using genome-wide SNPs. It was developed to simultaneously estimate the joint effects of all SNPs and the genetic architecture parameters for a complex trait, including SNP-based heritability, polygenicity and the joint distribution of effect sizes and minor allele frequencies.
Version 2.0 or above of the GCTB software includes summary-data-based versions of the individual-level data Bayesian linear mixed models previsouly implemented.
Credits
Jian Zeng developed the software with supports from Jian Yang, Futao Zhang and Zhili Zheng.
Part of the code are adopted from GCTA and GenSel.
Luke Lloyd-Jones contributed to the BayesR module with supports from Jian Zeng and Mike Goddard.
Jian Zeng, Zhili Zheng, and Shouye Liu contributed to the SBayesRC module.
Version 2.0 of the software was developed by Jian Zeng with contributions from Luke Lloyd-Jones, Zhili Zheng, and Shouye Liu.
Questions and Help Requests
If you have any bug reports or questions, please send an email to Jian Zeng (j.zeng@uq.edu.au).
Citation
Zeng et al. (2018) Signatures of negative selection in the genetic architecture of human complex traits. Nature Genetics, doi: 10.1038/s41588-018-0101-4.
SBayesRC
Zheng et al. (2024) Leveraging functional genomic annotations and genome coverage to improve polygenic prediction of complex traits within and between ancestries. Nature Genetics, doi: 10.1038/s41588-024-01704-y.
SBayesR
Lloyd-Jones, Zeng et al. (2019) Improved polygenic prediction by Bayesian multiple regression on summary statistics. Nature Communications, doi: 10.1038/s41467-019-12653-0.
SBayesS
Zeng et al. (2021) Bayesian analysis of GWAS summary data reveals differential signatures of natural selection across human complex traits and functional genomic categories. Nature Communications, dio: 10.1038/s41467-021-21446-3.
Download
Executable
gctb_2.5.2_Linux.zip (Lastest version updated in 20 June 2024)
Source code
Tutorial data
Eigen-decomposition data of LD matrices
The eigen-decomposition data are for SBayesRC and SBayesR with the low-rank model. In the follwoing link, we provide data derived from unrelated UKB individuals of Europan (EUR), East Asian (EAS), and African (AFR) ancestires. See our manuscript and Tutorial for details.
Functional genomic annotations
Download the formatted data for per-SNP functional annotations derived from S-LDSC BaselineLDv2.2.
LD matrices
The following LD matrices were computed based on 1.1 million common SNPs in a random sample of 50K unrelated individuals of European ancestry in UK Biobank dataset unless otherwise noted.
In the shrunk sparse matrices, described in Lloyd-Jones et al. (2019), the observed LD correlations computed from a reference sample were shrunk toward the expected values defined by a genetic map, following the algorithm in Wen and Stephens (2010). After shrinkage, LD correlations smaller than a threshold (default 1e-5) were set to be zero to give a sparse format, which is more efficient in storage and computation.
The sparse matrices described in Zeng et al. (2021) were computed by setting the likely chance LD to zero based on a chi-squared test (default threshold at chi-squared test statistic of 10).
While the shrunk sparse matrices were used in our original SBayesR paper, Prive et al. (2021) found that using a banded matrix with a window size of 3 cM per SNP can improve prediction accuracy. Therefore, we have created such a LD matrix in GCTB format for SBayesR analysis.
Summary data and PGS weights
The summary data for the 50 (including 28 approximately independent) UKB traits analysed in Zheng et al. 2022 can be downloaded here: summary data, and the corresponding PGS weights can be found here: PGS weights. The PGS weights are joint effect estimates derived from ~7 million genome-wide SNPs, therefore it’s important to have matched SNP set between training and validation datasets. This is because if some important SNPs present in the training are missing in the validation, the genetic effects captured by these SNPs will be lost. To maximise the utility of the joint SNP weights, we recommend considering genotype imputation or rerunning SBayesRC with the matched set of SNPs. In addition, note that the PGS weights were estimated using samples of the European ancestry, so they will perform best when applying to individuals of the European ancestry.
Older versions
gctb_2.5.1: [Linux executable] [source code]
gctb_2.05beta: [Linux executable] [source code]
gctb_2.04.3: [Linux executable] [source code]
gctb_2.03beta: [Linux executable] [source code]
gctb_2.02: [Linux executable]
gctb_2.0: [Linux executable] [source code] [MPI version source code]
gctb_1.0: [Linux executable] [Mac executable] [source code] [MPI version source code]
The MPI version implements a distributed computing strategy that scales the analysis to very large sample sizes. A significant improvement in computing time is expected for a sample size > 10,000. The MPI version needs to be compiled on user’s machine. See README.html in the tarball for instructions of compilation and usage. A testing dataset is also included in each tarball.
Update log
1. 1 Dec, 2017: first release.
2. 8 Feb, 2019: version 2.0 includes summary-data-based Bayesian methods.
3. 31 Jul, 2020: version 2.02 reports a message for convergence issue.
4. 15 Oct, 2021: version 2.03beta includes a robust parameterisation that attempts to address convergence issue.
5. 12 Dec, 2022: version 2.04.3 includes additional random effect component in BayesC and BayesR models to capture non-SNP random effects.
6. 11 April, 2023: version 2.05beta implements SBayesRC (SBayesR with the low-rank model) for polygenic prediction incorporating functional genomic annotations.
7. 29 April, 2024: version 2.5.1 adds functions for fine-mapping and to remove problematic SNPs during MCMC in SBayesRC.
8. 20 June, 2024: version 2.5.2 fixed bugs regarding -nan SigmaSq results and adds LD-based approach for computing credible sets.
Basic options
Input and output
--bfile test
Input PLINK binary PED files, e.g. test.fam, test.bim and test.bed (see PLINK user manual for details).
--pheno test.phen
Input phenotype data from a plain text file, e.g. test.phen.
--out test
Specify output root filename.
Data management
--keep test.indi.list
Specify a list of individuals to be included in the analysis.
--chr 1
Include SNPs on a specific chromosome in the analysis, e.g. chromosome 1.
--extract test.snplist
Specify a list of SNPs to be included in the analysis.
--exclude test.snplist
Specify a list of SNPs to be excluded from the analysis.
--mpheno 2
If the phenotype file contains more than one trait, by default, GCTB takes the first trait for analysis (the third column of the file) unless this option is specified. For example, --mpheno 2 tells GCTB to take the second trait for analysis (the fourth column of the file).
--covar test.qcovar
Input quantitative covariates from a plain text file, e.g. test.qcovar. Each quantitative covariate is recognized as a continuous variable.
--random-covar test.randcovar
Input quantitative covariates from a plain text file which will be fitted as random effects in the model. For a categorical variable with k levels, create a matrix of 0/1 with k columns to indicate the presence of each level in a column.
MCMC settings
--seed 123
Specify the seed for random number generation, e.g. 123. Note that giving the same seed value would result in exactly the same results between two runs.
--chain-length 21000
Specify the total number of iterations in MCMC, e.g. 21000 (default).
--burn-in 1000
Specify the number of iterations to be discarded, e.g. 1000 (default).
--out-freq 100
Display the intermediate results for every 100 iterations (default).
--thin 10
Output the sampled values for SNP effects and genetic architecture parameters for every 10 iterations (default). Only non-zero sampled values of SNP effects are written into a binary file.
--no-mcmc-bin
Suppress the output of MCMC samples of SNP effects.
Bayesian alphabet
--bayes S
Specify the Bayesian alphabet for the analysis, e.g. `S`. Different alphabet launch different models, which differ in the prior specification for the SNP effects. The available alphabet include
B: Each SNP effect is assumed to have an i.i.d. mixture prior of a t-distribution `t(0, \tau^2, \nu)` with a probability `\pi` and a point mass at zero with a probability `1-\pi`.
C: Each SNP effect is assumed to have an i.i.d. mixture prior of a normal distribution `N(0, \sigma^2)` with a probability `\pi` and a point mass at zero with a probability `1-\pi`.
S: Similar to C but the variance of SNP effects is related to minor allele frequency (`p`) through a parameter `S`, i.e. `\sigma_j^2 = [2p_j(1-p_j)]^S \sigma^2`.
N: nested BayesC. SNPs within a 0.2 Mb non-overlapping genomic region are collectively considered as a window (specify the distance by --wind 0.2). This nested approach speeds up the analysis by skipping over windows with zero effect.
NS: nested BayesS.
R: BayesR. Each SNP effect is assumed to have an i.i.d. mixture prior of multiple normal distributions `N(0, \gamma_k \sigma_k^2)` with a probability `\pi_k` and a point mass at zero with a probability `1-\sum_k \pi_k`, where `\gamma_k` is a given constant.
--fix-pi
An option to fix `\pi` to a constant (the value is specified by the option --pi below). The default setting is to treat π as random and estimate it from the data.
--pi 0.05
A starting value for the sampling of π when it is estimated from the data, or a given value for π when it is fixed. The default value is 0.05. When BayesR is used, it is a string seperated by comma where the number of values defines the number of mixture components and each value defines the starting value for each component (the first value is reserved for the zero component); the default values are 0.95,0.03,0.01,0.01.
--gamma 0,0.01,0.1,1
When BayesR is used, this speficies the gamma values seperated by comma, each representing the scaling factor for the variance of a mixture component. Note that the number of values should match that in --pi.
--hsq 0.5
A starting value for the sampling of SNP-based heritability, which may improve the mixing of MCMC algorithm if it starts with a good estimate. The default value is 0.5.
--S 0
A starting value for the sampling of the parameter S (relationship between MAF and variance of SNP effects) in BayesS, which may improve the mixing of MCMC algorithm if it starts with a good estimate. The default value is 0.
--wind 0.2
Specify the window width in Mb for the non-overlapping windows in the nested models, e.g. 0.2 Mb. The default value is 1 Mb.
--var-random 0.05
Specify the prior knowledge on the proportion of variance explained by the non-SNP random effects. This value will be used to specify the prior distribution for the non-SNP random effect variance variable.
Examples
Standard version of gctb:
gctb --bfile test --pheno test.phen --bayes S --pi 0.1 --hsq 0.5 --chain-length 25000 --burn-in 5000 --out test > test.log 2>&1
MPI version of gctb (when using intelMPI libraries and two nodes):
mpirun -f $PBS_NODEFILE -np 2 gctb_mpi --bfile test --pheno test.phen --bayes S --pi 0.1 --hsq 0.5 --chain-length 25000 --burn-in 5000 --out test > test.log 2>&1
The output files include:
test.log: a text file of running status, intermediate output and final results;
test.snpRes: a text file of posterior statistics of SNP effects;
test.covRes: a text file of posterior statistics of covariates;
test.parRes: a text file of posterior statistics of key model parameters;
test.mcmcsamples.CovEffects: a text file of MCMC samples for the covariates fitted in the model;
test.mcmcsamples.SnpEffects: a binary file of MCMC samples for the SNP effects;
test.mcmcsamples.Par: a text file of MCMC samples for the key model parameters;
Citations
GCTB software and BayesS method
Zeng et al. (2018) Signatures of negative selection in the genetic architecture of human complex traits.
Nature Genetics, doi: 10.1038/s41588-018-0101-4.
BayesR
Moser et al. (2015) Simultaneous discovery, estimation and prediction analysis of complex traits using a Bayesian mixture model. PLoS Genetics, 11: e1004969.
BayesN
Zeng et al. (2018) A nested mixture model for genomic prediction using whole-genome SNP genotypes. PLoS One, 13: e0194683.
BayesC`\pi`
Habier et al. (2011) Extension of the Bayesian alphabet for genomic selection. BMC Bioinformatics, 12: 186.
BayesB
Meuwissen et al. (2001) Prediction of total genetic value using genome-wide dense marker maps. Genetics, 157: 1819-1829.
Summary Bayesian Alphabet
--sbayes R
Available models are R, S and C.
--ldm test.ldm.sparse
Input the LD matrix generated by --make-sparse-ldm option. This option tells GCTB to read two files: a text file that contains SNP information (test.ldm.sparse.info) and a binary file that contains the sparse LD matrix data (test.ldm.sparse.bin). The suffix ".sparse" tells GCTB the format of the LD matrix. The valid suffixes include ".full", ".band", ".shrunk" and ".sparse", which are generated from the corresponding options that make the LD matrix in sush a format, e.g. --make-full-ldm for ".full" files.
--mldm mldm.list
Input a list of LD matrices, e.g. from chromosome 1 to 22. The LD matrices need to be in the correct order in mldm.list.
--make-full-ldm
Compute a full LD matrix from the genotype data provided by --bfile option. This option will generate two files: a text file that contains SNP information (test.ldm.full.info) and a binary file that contains the full LD matrix data (test.ldm.full.bin). The full LD matrix contains all pairwise LD correlations between SNPs. The memory required is approximately the size of the n-by-m genotype matrix (4 * n * m)/1e9 GB + the size of the m-by-m LD matrix (4 * m^2)/1e9 GB (n is the number of individuals and m is the number of SNPs). For a more efficient computation, it is recommended to use --snp option to compute the matrix by parts.
--part 5,1
Work only with --make-full-ldm. Compute a full LD matrix part by part to save memory. The first number before comma indicates the total parts to divide, the second number indicates the current part to calculate. Run gctb with the --mldm output.mldm to merge, after all parts are calculated successfully.
--make-sparse-ldm
Compute a sparse LD matrix from the genotype data provided by --bfile option or from the dense type LD matrix, such as full or shrunk LD matrix provided by --ldm test.ldm.full or --ldm test.ldm.shrunk option. If the genotype data is provided, GCTB will first compute the chromosome-wide full LD matrix, then set the chance LD (small LD correlations due to sampling) to be zero and output the sparse matrix. The chance LD is detected by a chi-squared test with the threshold defined by --chisq. The chi-squared threshold value is 10 by default. The memory usage is the same as computing a full LD matrix.
--make-shrunk-ldm
Compute a shrunk LD matrix from the genotype data provided by --bfile option or from the full LD matrix provided by --ldm test.ldm.full option. It will use the method proposed by Wen and Stephens (2010) to shrunk the off-diagonal entries of the sample LD matrix toward zero based on a genetic map provided by --gen-map option (see Tutorial for the format of the genetic map). Other parameters required by the shrinkage method include the effective population size provided by --ne option (default value is 11400), the genetic map sample size provided by --genmap-n option (default value is 183) and the shrinkage cutoff threshold provided by --shrunk-cutoff option (default value is 1e-5). The output format of the shrunk LD matrix is ".shrunk", which contains all the zero elements, so it will take a similar storage space as the full LD matrix. We recommend to further make the shrunk LD matrix parse by eliminating elements equal to zero for efficient storage and computation, which can be done by reading the generated shrunk matrix and making it sparse using --make-sparse-ldm --chisq 0 options. The memory usage is the same as computing a full LD matrix.
--make-band-ldm
Compute a banded LD matrix from the genotype data provided by --bfile option or from the full LD matrix provided by --ldm test.ldm.full option. GCTB will only compute and include the LD correlations between all paris of SNPs within a sliding window which has a window width defined by --wind option (in the unit of megabase).
--snp 1-5000
Compute the LD matrix by rows (or columns as it is a symmetric square matrix). When this option is invoked, GCTB will read in the genotype matrix from the bed file and compute a part of the LD matrix corresponding to the range of SNPs specified. GCTB will append .snp1-5000, for example, to the output files. Once all parts have been computed individually, make sure to include all the files as a list in the ascending order as a separate file and use --mldm option to merge the parts into a single matrix. See Toturial for more detail.
--gwas-summary test.ma
Input the GWAS summary statistics in the GCTA-COJO .ma format.
SNP A1 A2 freq b se p N
rs1001 A G 0.8493 0.0024 0.0055 0.6653 129850
rs1002 C G 0.0306 0.0034 0.0115 0.7659 129799
rs1003 A C 0.5128 0.0045 0.0038 0.2319 129830
Columns are SNP identifier, the effect allele, the other allele, frequency of the effect allele, effect size, standard error, p-value and sample size. The headers are not keywords and will be omitted by the program. Important: "A1" needs to be the effect allele with "A2" being the other allele and "freq" should be the frequency of "A1". See Tutorial for more information.
--chisq 10
Specify the chi-squared test threshold for computing the sparse LD matrix. The LD correlations that are less than the threshold (default value is 10) is regarded due to sampling variation and therefore removed from the LD matrix. It is equivalent to setting the LD rsq smaller than (chi-squared threshold)/(LD reference sample size).
--ld 0.01
Specify the absolute value of LD correlation threshold for computing the sparse LD matrix. Any absolute value of the LD correlation below the threshold will be set to be zero. It cannot be used together with --chisq.
--write-ldm-txt
Output the LD matrix in a text file.
--annot annotation.txt
Input the genomic annotation data and launch the stratified SBayes analysis (SBayesS-strat). The format of the annotation file is as below.
SNP Coding Conserved DHS Promoter
rs1001 0 1 0 0 0
rs1002 1 0 0 0 0
rs1003 0 0 0 1 1
The first column is the SNP identifier, followed by annotation categories. The first row is the header line that contains the names of the annotation categories. The current version only allows binary annotations (i.e. 0/1) and only available for SBayesS model (i.e. together with --sbayes S option), which allows the SNP-heritability, polygenicity and the S parameter (relationship between effect size and MAF) to be different across annotation categories.
--exclude-mhc
This option will remove SNPs in the MHC regions (chr6:28-34 Mb) from the analysis.
--ambiguous-snp
This option will remove SNPs with ambiguous nucleotides, i.e. A/T or G/C.
--maf 0.01
This option will remove SNPs with minor allele frequency from the GWAS sample smaller than the specified value.
--overlap
This option tells GCTB that the LD reference sample is in complete overlap with the GWAS sample. That is, the LD matrix is computed from the GWAS sample itself. This will suppress the modeling of sampling variance of LD correlations in the Sbayes analysis.
--impute-n
This option will impute per-SNP sample size in GWAS based on the GWAS effect estimates, SE and allele frequencies in the .ma file, and remove SNPs with the imputed sample size greater/smaller than 3 standard deviations from the median value.
--num-chains 4
This option invokes a multi-chain MCMC process, e.g. 4 chains. GCTB will run multiple chains in sequence each with the starting values of the model parameters randomly sampled from their prior distributions. When the MCMC chains are completed, it will calculate the Gelman-Rubin convergence diagnostic (also known as potential scale reduction factor) for each of the model parameters and report them in the .parRes file. For example,
Posterior statistics from multiple chains:
Mean SD R_GelmanRubin
Pi 0.044129 0.001628 1.005
NnzSnp 49875.335938 1825.153442 1.005
SigmaSq 0.000009 0.000000 1.007
S -0.545913 0.029914 1.003
ResVar 0.727659 0.002897 1.000
GenVar 0.257742 0.002645 1.000
SigmaSqG 0.258967 0.003865 1.000
hsq 0.261560 0.002507 1.000
In the current verion, the multi-chain MCMC is only available for SBayesC, SBayesS and SBayesS-strat analysis.
--rsq 0.9
For a pair of SNPs with the squared LD correlation greater than the specified value, e.g. 0.9, based on the provided LD matrix, this option will remove the SNP with the higher GWAS P value and keep the other SNP in the analysis.
--p-value 0.4
This option will remove SNPs with GWAS P value greater than the specified value, e.g. 0.4, from the analysis.
--robust
This option will invoke the following parameterisation for the common factor of SNP effect variance in SBayesR, i.e., \$\sigma_{\beta}^2 = \frac{\sigma_g^2 }{ m {\boldsymbol \gamma}'{\boldsymbol \pi} }\$ where \$\sigma_g^2 = {\boldsymbol \beta} ' {\bf R} {\boldsymbol \beta}\$ is the sampled total genetic variance in each MCMC iteration. Comparing to the original model that assumes \$\sigma_{\beta}^2\$ following a scaled-inverse chi-square distribution, this parameterisation is observed to be more robust to the potential convergence issue which sometimes occurs when the GWAS summary statistics are from a meta-analysis. In GCTB 2.03 beta version, the program will start with the original model but if a convergence issue is detected (indicated by a negative sampled value of residual variance) it will restart the MCMC process with this more robust parameterisation. Note that this parameterisation is identical to LDpred (Vilhjálmsson et al. 2015) when using a point-normal prior (i.e., two-component SBayesR or SBayesC).
--hsq-percentage-model true
If you run SBayesR using GCTB v2.5.1 or above, the default model is the heritability percentage model, i.e., a mixture of normal distributions with the variance equal to \$\gamma_k %\$ of the estimated SNP-based heritability. To switch to the model described in the SBayesR paper, which considers the variance component \$\sigma_\beta^2\$ as a free parameter, set the value to be 'false'.
Tutorial
SBayesR Tutorial
This updated version of the GCTB software (version 2.0) includes summary-data based versions of the individual-data Bayesian linear mixed models previously implemented. These methods require summary statistics from genome-wide association studies, which typically include the estimated univariate effect for each single nucleotide polymorphism (SNP), the standard error of the effect, the sample size used to estimate the effect for each SNP, the allele frequency of an allele, and an estimate of LD among SNPs, all of which are easily accessible from public databases.
This tutorial will outline how to use the summary data based methods and accompanies the manuscript Improved polygenic prediction by Bayesian multiple regression on summary statistics. To recreate the tutorial you will need the PLINK 2 software and the updated version of the GCTB software compiled from source or the binary executable in your path. The data for the tutorial are available at Download. The tutorial is designed so that each part can be reconstructed or picked up at any point with the following directory structure.
tutorial
gctb # Static binary executable for Linux 64-bit systems
data # 1000 Genomes data in PLINK format
pheno_generation # R scripts for generating simulated phenotypes
pheno # Simulated phenotypes
gwas # PLINK GWAS summary statistics
ldm # LD correlation matrices and scripts to calculate them
ma # Summary statistics in GCTB compatible format
sbayesr # Scripts for running and SBayesR analysis using GCTB and subsequent results
Data
The tutorial will run through all aspects of the software using genotype data from chromosome 22 of Phase 3 of the 1000 Genomes Project (1000G). The genotype data have been filtered to exclude variants with minor allele frequency (MAF) < 0.01, which left 15,938 SNPs available for analysis. These data include a subset of 378 individuals of European ancestry from the CEU, TSI, GBR and FIN populations.
N.B. The results generated from this example tutorial using data from the 1000G are designed to be lightweight and should be only used to explore how to run summary data based analyses using GCTB. The results do not make the best use of GCTB capabilities given the small sample size \$(N=378)\$ in the example.
Phenotype simulation and GWAS
Using these genotypes, phenotypes were generated under the multiple regression model \$y_i = \sum_{j=1}^pw_{ij}\beta_j + \epsilon_i\$, where \$w_{ij} = (x_{ij} − 2q_j)/ \sqrt{2q_j(1 − q_j)}\$
with \$x_{ij}\$ being the reference allele count for the \$i\$th individual at the \$j\$th SNP, \$q_j\$ the allele
frequency of the \$j\$th SNP and \$\epsilon_i\$ was sampled from a normal distribution with mean 0 and variance
\$\text{Var}({\bf W}\boldsymbol\beta)(1/h_{SNP}^2 − 1)\$ such that \$h_{SNP}^2 = 0.1\$ for each of 20 simulation replicates,
which is much larger than the contribution to the genome-wide SNP-based heritability (\$h^2_{SNP}\$) estimate for chromosome 22
for most quantitative traits. All phenotypes were generated using the R programming language with scripts used available in the
pheno_generation subdirectory.
For each scenario replicate, we randomly sampled a new set of 1,500 causal variants. The genetic architecture simulated contained two causal variants of large effect explaining 3% and 2% of the phenotypic variance respectively and a polygenic tail of 1,498 causal variants sampled from a N(0, 0.05/1, 498) distribution such that the expected total genetic variance explained by all variants was 0.1.
For each of the 20 simulation replicates, simple linear regression for each variant was run using the PLINK 2 software to generate summary statistics. Code for running the GWAS and the output is available in the gwas subdirectory.
GCTB summary statistics input format
The GCTB summary-based methods have inherited the GCTA-COJO .ma format.
SNP A1 A2 freq b se p N
rs1001 A G 0.8493 0.0024 0.0055 0.6653 129850
rs1002 C G 0.0306 0.0034 0.0115 0.7659 129799
rs1003 A C 0.5128 0.0045 0.0038 0.2319 129830
Columns are SNP identifier, the effect allele, the other allele, frequency of the effect allele, effect size, standard error, p-value and sample size. The headers are not keywords and will be omitted by the program. Important: "A1" needs to be the effect allele with "A2" being the other allele and "freq" should be the frequency of "A1".
The transformation of your summary statistics file to the .ma format will depend on the software used to analyse your data. The
ma subdirectory contains a simple R script for constructing .ma files from PLINK 2 --linear output. There is no need to filter
you summary statistics to match the LD reference as GCTB will perform this data management for you.
GCTB linkage disequilibrium (LD) correlation matrix
The construction of an LD correlation matrix is a key component of the summary-data based methods in GCTB. Theoretically, the summary-data based methods are equivalent to the individual data methods if the LD matrix is constructed from all variants and the individuals used in the GWAS. Calculating and storing LD matrices that contain all pairwise entries is computationally prohibitive and thus a subset of the matrix entries are stored. Typically, all inter-chromosomal LD is ignored and a within chromosome block diagonal matrix structure is used. Futhermore, the individual level data from the GWAS is not available, which is often the case, and a reference population that is similar in ancestry to the GWAS cohort is used to construct the LD correlation matrix. The use of a subset of the correlation matrix and the construction of the LD matrix from a reference leads to an approximation to the individual data mode. The level of deterioration in the model parameter estimates introduced by these approximations is assessed empirically through simulation, real data analysis and comparison with individual-data method estimates.
Full chromosome-wise LD matrices
Although possible to create genome-wide LD matrices in GCTB, we recommend to only
calculate matrices for each chromosome. The following is the basic execution of
GCTB LD matrix calculation. The ldm subdirectory has example BASH scripts to
perform this on a HPC system. N.B. the HPC commands may not be compatible with your HPC scheduler
and will require alteration.
# Build full LD matrix for chromosome 22
gctb --bfile 1000G_eur_chr22 --make-full-ldm --out 1000G_eur_chr22
GCTB produces a .bin file, which contains the matrix elements stored in binary, and a .info
file, which looks like
Chrom ID GenPos PhysPos A1 A2 A2Freq Index WindStart WindEnd WindSize WindWidth N SamplVar LDsum
22 rs131538 0 16871137 A G 0.066138 0 0 15937 15938 34347869 378 41.92552 10.18005
22 rs9605903 0 17054720 C T 0.264550 1 0 15937 15938 34347869 378 41.95537 -33.15312
22 rs5746647 0 17057138 G T 0.052910 2 0 15937 15938 34347869 378 41.93396 15.90974
22 rs16980739 0 17058616 T C 0.148148 3 0 15937 15938 34347869 378 41.94403 -12.93685
The columns headings are chromosome, SNP identifier, genetic position, physical base pair position, SNP allele 1, SNP allele 2, frequency of the A2 allele, variant index, for this SNP (row) the first column that is non-zero in the LD matrix, the last column that is non-zero, how many non-zero elements for this row, difference in base pair position between WindStart and WindEnd, the sample size used to calculate the correlation, sum of samping variance of the LD correlation estimate for the SNP and all other SNPs on the chromosome and the sum of the non-zero LD correlation estimates between this SNP and all other SNPs.
Full chromosome-wise LD matrices using multiple CPUs
To reduce the computational burden of computing LD correlation matrices, GCTB can partition the genotype file into user-specified chunks.
# Build full LD matrix for chromosome 22 for the first 5000 variants
gctb --bfile 1000G_eur_chr22 --make-full-ldm --snp 1-5000 --out 1000G_eur_chr22
When the --snp option is invoked the GCTB software will append .snp1-5000, for example, to the output files
so no separate extension to --out is required.
For the 1000G chromsome 22 example the following files are generated
1000G_eur_chr22.snp1-5000.ldm.full.bin
1000G_eur_chr22.snp1-5000.ldm.full.info
1000G_eur_chr22.snp5001-10000.ldm.full.bin
1000G_eur_chr22.snp5001-10000.ldm.full.info
1000G_eur_chr22.snp10001-15000.ldm.full.bin
1000G_eur_chr22.snp10001-15000.ldm.full.info
1000G_eur_chr22.snp15001-20000.ldm.full.bin
1000G_eur_chr22.snp15001-20000.ldm.full.info
To merge the files, a separate file with the list of files to be joined is required. For our example is looks like
cat 1000G_eur_chr22.mldmlist
1000G_eur_chr22.snp1-5000.ldm.full
1000G_eur_chr22.snp5001-10000.ldm.full
1000G_eur_chr22.snp10001-15000.ldm.full
1000G_eur_chr22.snp15001-20000.ldm.full
# Merge the LD matrix chunks into a single file
gctb --mldm 1000G_eur_chr22.mldmlist --make-full-ldm --out 1000G_eur_chr22
Shrunk LD matrix
The shrinkage estimator for the LD correlation matrix was originally proposed by Wen and Stephens (2010). The estimator shrinks the off-diagonal entries of the sample LD matrix toward zero. Zhu and Stephens (2017) used the shrinkage estimator in their Regression with Summary Statistics (RSS) methodology and showed empirically that it can provide improved inference. The shrinkage estimator overcomes some of the issues arising from approximating the full LD matrix in the summary-data based model using a subset of the full LD matrix and constructing the matrix from a reference. The GCTB implementation is a C++ port from that provided with the RSS software and has been adapted for use with the GCTB software.
The calculation of the LD correlation matrix shrinkage estimate requires a genetic map. The genetic map files can be provided by the user but the tutorial uses interpolated map positions for the CEU population generated from the 1000G OMNI arrays that were downloaded from the from https://github.com/joepickrell/1000-genomes-genetic-maps. The file format looks like
rs149201999 16050408 0.0
rs146752890 16050612 0.0
rs139377059 16050678 0.0
rs188945759 16050984 0.0
rs6518357 16051107 0.0
rs62224609 16051249 0.0
rs62224610 16051347 0.0
rs143503259 16051453 0.0
rs192339082 16051477 0.0
rs79725552 16051480 0.0
and contains SNP identifier, physical base pair position and genetic position (cumulative). GCTB can use any genetic map provided it adheres to this format.
In this tutorial, the calculation of the shrunk LD matrix requires the effective population sample size, which we set to be 11,400 (as in Zhu and Stephens (2017)), the sample size of the genetic map reference, which corresponds to the 183 individuals from the CEU cohort of the 1000G used to create the genetic map, and the hard threshold on the shrinkage value, which we set to \$10^{−5}\$ and is the default value. These three parameters can be changed with
--ne # Effective population size. Default is 11,400
--genmap-n # Genetic map sample size. Default is 183
--shrunk-cutoff # Shrinkage hard threshold. Default is 10^-5
The constuction of the shrunk LD matrix is similar to that for the full LD matrix
# Build shrunk LD matrix for chromosome 22
gctb --bfile 1000G_eur_chr22 \
--make-shrunk-ldm \
--gen-map chr22.OMNI.interpolated_genetic_map \
--out 1000G_eur_chr22
The GCTB can also perform shrunk matrix calculation using multiple CPUs with a similar process to the above calculation of the full LD matrix.
# Build shrunk LD matrix for chromosome 22 for the first 5000 variants
gctb --bfile 1000G_eur_chr22 \
--make-shrunk-ldm \
--gen-map chr22.OMNI.interpolated_genetic_map \
--snp 1-5000 \
--out 1000G_eur_chr22
Please see the /ldm subdirectory for example BASH scripts of performing these tasks
both locally and on a HPC.
Sparse LD matrix
Motivated by the computational practicality of not storing the genome-wide LD correlation matrix we wish to set a subset of elements of the LD correlation to zero. The calculation of an LD correlation matrix from genotype data is an estimate of the true LD correlation matrix for a population. It therefore contains a mix of true LD and those values that differ from zero due to sampling variation, which we wish to ignore. By default we ignore interchromsomal LD between markers. Within chromosome, we set elements to zero if their chi-squared statistic under the sampling distribution of the correlation coefficient does not exceed a user-chosen threshold.
Specifically, from \citet{lynch1998genetics} the sampling variation of the correlation coefficient \$r = \frac{\text{cov}(x, y)}{[\text{var}(x)\text{var}(y)]^{1/2}}\$ is
\$\sigma^2(r) \approx \frac{(1-\rho^2)^2}{n}\$, which under the null hypothesis that \$\rho = 0\$ is just \$\frac{1}{n}\$. Given this we can
generate a chi-squared statistic for each element of the LD matrix by \$(\frac{r}{\sqrt{1/n}})^2\$. These statistics should be \$\chi_1^2\$ distributed
and thus for each LD matrix element we set it to zero if the statistic does not exceed a user-specified arbitrary value. The chi-squared
statistic can be altered with --chisq. The default value is 10, which we have found empirically to be a good balance balance between
matrix sparsity and retaining true positive LD values.
# Build sparse LD matrix for chromosome 22
gctb --bfile 1000G_eur_chr22 --make-sparse-ldm --out 1000G_eur_chr22
# Sparse matrices can also be built using multiple CPUs
gctb --bfile 1000G_eur_chr22 --make-sparse-ldm --snp 1-5000 --out 1000G_eur_chr22
GCTB can alter current LD matrices, for example, make a full matrix sparse.
# Make a full LD matrix sparse
gctb --ldm 1000G_eur_chr22.ldm.full --make-sparse-ldm --out 1000G_eur_chr22
We recommend that the shrunk LD matrices be stored in sparse format for efficient storage and computation. The shrunk LD correlation matrix estimate will have zeroes which can be eliminated as follows
# Make a shrunk LD matrix sparse by eliminating elements equal to 0. Output sparse
gctb --ldm 1000G_eur_chr22.ldm.shrunk --make-sparse-ldm --chisq 0 --out 1000G_eur_chr22
Extra options for LD matrix calculation
# For checking or comparison with other methods you can write the LD correlation out in
# text format.
--write-ldm-txt # Write LD matrix as text file as well as binary. Will generate large files.
# Examples
gctb --bfile 1000G_eur_chr22 --make-shrunk-ldm --write-ldm-txt --out 1000G_eur_chr22
gctb --bfile 1000G_eur_chr22 --make-full-ldm --write-ldm-txt --out 1000G_eur_chr22
# Read a list of LD matrix files. This would be used to read the list of chromosome wise LD
# matrices when performing genome-wide analyses. Also used for merging matrix chunks for
# multiple CPU matrix building
--mldm
Running an SBayesR analysis
With the GWAS summary statistics in .ma format and the LD correlation matrix calculated, an SBayesR analysis can be performed by
# Calling SBayesR
gctb --sbayes R
--ldm ../ldm/sparse/chr22/1000G_eur_chr22.ldm.sparse
--pi 0.95,0.02,0.02,0.01
--gamma 0.0,0.01,0.1,1
--gwas-summary ../ma/sim_1.ma
--chain-length 10000
--burn-in 2000
--out-freq 10
--out sim_1
--sbayes R
Specify the summary data based Bayesian alphabet model for the analysis, e.g., R. Different letters of the alphabet launch
different models, which differ in the prior specification for the SNP effects. R and C are currently available.
--pi 0.95,0.02,0.02,0.01
Specific to the R model. A comma seperated string where the number of values defines the number of mixture components and each value defines the starting value for each component (the first value is reserved for the zero component).
These must sum to 1.
The length of the \$\pi\$ and \$\gamma\$ vectors stipulates how many components are included in the finite mixture of normals distribution prior
for the genetic effects. The default values are as specified in the example.
--gamma 0,0.01,0.1,1
Specific to the R model. Speficies the gamma values seperated by comma, each representing the scaling factor for the
the variance of the distribution of genetic effects \$\sigma_{\beta}^2\$ for each distribution. Note that the vector length should match
that in --pi. The default values are as specified in the example. These differ from the original BayesR model as the
weights are for the variance of the distribution of genetic effects \$\sigma_{\beta}^2\$ rather than the genetic variance \$\sigma_g^2\$.
--gwas-summary
Path to the GWAS summary statistics in .ma format.
The other options are inherited from the individual-data GCTB models.
Standard output
Upon execution of GCTB, preliminary data management information will be outputted to standard out. A key summary of the summary is also displayed, for example,
Data summary:
mean sd
GWAS SNP Phenotypic variance 1.002 0.052
GWAS SNP sample size 378 0
GWAS SNP effect 0.000 0.117
GWAS SNP SE 0.106 0.049
MME left-hand-side diagonals 379.478 19.774
MME right-hand-side 0.130 19.983
LD sampling variance 1.298 0.076
LD score 17.359 15.140
These statistics can be used to diagnose errors between individual runs of the program.
For each row the mean and standard deviation (sd) of the parameter distribution are displayed. The
acronym MME represents mixed model equations. The left-hand-side diagonals
are the elements of \${\bf D}=\text{diag}({\bf X'}{\bf X})\$, where \$D_j=2p_jq_jn_j\$
under Hardy-Weinberg equilibrium and \$n_j\$ is the sample
size of variant \$j\$. The right-hand-side is equal to \${\bf Db}\$ where \${\bf b}\$ is the \$p\times 1\$ vector of marginal
effect estimates from GWAS. LD sampling variance and LD score are
as described in the .info file.
Post launch of a summary data model the sampled values of key model parameters are printed to standard out in real time. For example, during an SBayesR analysis the following snapshot shows what is being printed
Iter Pi1 Pi2 Pi3 Pi4 NnzSnp SigmaSq ResVar GenVar hsq Rounding TimeLeft
10 0.9513 0.0162 0.0170 0.0155 795 0.0001 0.8905 0.0260 0.0284 0.0000 0:16:39
20 0.9507 0.0112 0.0172 0.0208 761 0.0001 0.9421 0.0213 0.0221 0.0000 0:8:19
30 0.9479 0.0041 0.0201 0.0279 761 0.0000 0.9747 0.0249 0.0249 0.0000 0:5:32
40 0.9448 0.0046 0.0187 0.0319 865 0.0000 0.9117 0.0203 0.0218 0.0000 0:4:9
50 0.9445 0.0054 0.0228 0.0272 893 0.0000 1.0019 0.0223 0.0218 0.0000 0:6:38
60 0.9409 0.0019 0.0223 0.0349 930 0.0000 1.0481 0.0265 0.0247 0.0000 0:5:31
The parameters printed are iteration number, which can be altered with --out-freq, proportion
of variants in distribution one (zero component) to four (can be altered by changing the \$\pi\$
and \$\gamma\$ vector lengths), number of non-zero effects in the model at iteration \$i\$,
the variance of the distribution of genetic effects \$\sigma_{\beta}^2\$, the residual variance
\$\sigma_{\epsilon}^2\$, the genetic variance \$\sigma_{g}^2\$ SNP-based heritability, rounding accumulation (a value
substantially greater than zero indicates insufficent machine precision and the user should consider terminating the
program), and an estimate of
the time left to complete the analysis. Upon completion of the analysis a summary of the
posterior mean and standard deviation of the key models parameters is reported to standard
out
Posterior statistics from MCMC samples:
Mean SD
Pi1 0.942564 0.006791
Pi2 0.056959 0.006728
Pi3 0.000305 0.000274
Pi4 0.000172 0.000094
NnzSnp 1726.798706 199.570724
SigmaSq 0.002898 0.000375
ResVar 0.900596 0.004205
GenVar 0.103104 0.002216
hsq 0.102722 0.002039
The output files are the same as those from the individual data models and include:
test.log: # Text file of running status, intermediate output and final results
test.snpRes: # Text file of posterior statistics of SNP effects
test.parRes: # Text file of posterior statistics of key model parameters
test.mcmcsamples.SnpEffects: # Binary file of MCMC samples for the SNP effects
test.mcmcsamples.Par: # Text file of MCMC samples for the key model parameters
Extra commands for running SBayes analyses
--unscale-genotype # Run analyses assuming genotypes are not scaled to unit variance. Default is scaled genotypes
--exclude-mhc # Exclude variants in the Major Histocompatibility Complex from the analysis. Highly recommended
# when performing genome-wide analyses
--exclude-region # Path to file where each line had three entries: chromosome, starting base pair position of
# region and end base pair of region
--impute-n # Let GCTB impute the sample size for each variant using an algoirithm if you cannot trust
# the sample size reported. Filters variants with a sample size further than 3 SD from the median of
# the sample size distribution. The method assumes each SNP has been calculated from the same set
# of individuals.
Summary
The method implemented in GCTB assumes certain ideal data constraints such as summary data computed from a single set of individuals at fully observed genotypes as well as minimal imputation error and data processing errors such as allele coding and frequency mismatch. Summary data in the public domain often substantially deviate from these ideals and can contain residual population stratification, which is not accounted for in this model. Practical solutions to these ideal data deviations include the use of data that are imputed and the restriction of analyses to variants that are known to be imputed with high accuracy. We found that the simple filtering of SNPs with sample sizes that deviate substantially from the mean across all variants from an analysis, when using summary statistics from the public domain substantially improved model convergence. However, even the reported sample size cannot be trusted in some summary data sets.
We explored LD pruning of variants to remove variants in very high LD (\$R^2>0.99\$) but found that this did not substantially improve model convergence or parameter estimates although this was not formally assessed. However, removal of high LD regions, such as the MHC region improved model convergence for real traits. High LD regions are expected to have the potential to be extreme sources of model misspecification with the model expecting summary data in to be very similar for variants in high LD. Small deviations due to data error not expected in the model likelihood at these loci thus have high potential to lead to model divergence (see Zhu and Stephens\citep{zhu2017bayesian} for further discussion). We strongly recommend reading the current manuscript and that of Zhu and Stephens (2017) as a preliminary to running the summary data based methods in GCTB.
SBayesRC Tutorial
SBayesRC is a method that incorporates functional genomic annotations with high-density SNPs (> 7 millions) for polygenic prediction. Our manuscript is available at here.
This method is based on a low-rank approximation which utilises the eigenvalues and eigenvectors of block-wise LD correlation matrices. It requires SNPs that are included in the LD reference to be also present in the GWAS samples. Thus, the first step is to impute the GWAS summary statistics for any missing SNPs that are only present in the LD reference. If there are more than 30% of missing SNPs, we recommend to recompute the eigen-decomposition based on a matched LD reference sample (see below).
Input files
ldm is a folder comprising the eigen-decomposition data for each block. We have provided the data from a random sample of 20K unrelated UKB individuals of European ancestry using either ~1 million HapMap3 SNPs or 7 million imputed SNPs, which are available at Download.
test.ma is the file of GWAS summary statistics with the following format
SNP A1 A2 freq b se p N
rs1001 A G 0.8493 0.0024 0.0055 0.6653 129850
rs1002 C G 0.0306 0.0034 0.0115 0.7659 129799
rs1003 A C 0.5128 0.0045 0.0038 0.2319 129830
annot.txt is the annotation file, with columns being SNP ID, Intercept (a column of one), and annotation values. You can include an arbitary number of annotations.
SNP Intercept Anno1 Anno2 Anno3
rs1001 1 1 0 0.2
rs1002 1 0 1 -1.5
rs1003 1 1 1 0.7
Step 1: QC & imputation of summary statistics for SNPs in LD reference but not in GWAS data.
gctb --ldm-eigen ldm --gwas-summary test.ma --impute-summary --out test --thread 4
This command will generate a text file test.imputed.ma which contains the summary statistics for all SNPs including those from the original GWAS file and those with imputed summary data. Use this file as input for the next step. --thread 4 enables multi-thread (e.g., 4 threads) computing and if it is ignored, a single thread will be used. Before imputation, a QC step is carried out to match alleles between GWAS and reference samples and remove SNPs with per-SNP sample size beyond 3 standard deviation acround the median in GWAS.
Tips for parallel computing: The imputation step is fully available for parallel computing across blocks and the runtime is expected to decrease linearly with the number of threads, so you can use as many cores as possible in your own computing platform. Alternatively, for the best efficiency, you can impute each block separately by using --block $i where i starts from 1 to the total number of blocks:
gctb --ldm-eigen ldm --gwas-summary test.ma --impute-summary --block $i --out test
This command will generate a text file test.block$i.imputed.ma for each block. After all blocks are finished, use the following command to merge all .ma files across block into a single file with genome-wide SNPs:
gctb --gwas-summary test --merge-block-gwas-summary --out test.imputed
Step 2: Run SBayesRC with annotation data.
gctb --ldm-eigen ldm --gwas-summary test.imputed.ma --sbayes RC --annot annot.txt --out test --thread 4
This command will generate a text file for SNP effect estimates test.snpRes, text files for model parameters test.parRes and test.parSetRes, and a folder that stores the MCMC samples for all model parameters test.mcmcsamples.
Predicting polygenic scores.
PLink can be used to produce polygenic score for the target cohort, using columns of test.snpRes as input. For example,
plink --bfile target --score test.snpRes 2 5 8 header sum center --out target
Recomputing eigen-decomposition of block-wise LD matrics
In the case where eigen-decomposition needs to be performed, e.g., the GWAS data is genetically different from our LD reference, or GWAS SNPs are substantially different from our LD reference SNPs, you can use the following steps to generate the eigen-decompostion data based on your own LD reference sample:
Step 1: compute block-wise LD matrices
Skip this step if you are using the eigen-decomposition data provided by us. This step requires individual-level genotype data from LD reference ldRef and a text input file that defines the boundaries of each block. Here, we use text file ref4cM_v37.pos which partitions the human genome into 591 approximately independent LD blocks, each with a width of at least 4 cM, based on the results of Berisa and Pickrell.
gctb --bfile ldRef --make-block-ldm --block-info ref4cM_v37.pos --out ldm --thread 4
This command will generate a folder called ldm as specified by --out. This folder will contain a serise of binary files for blocks block*.ldm.bin, a text file for genome-wide SNP information snp.info, and a text file for block information ldm.info. You can use --write-ldm-txt to print the content in the binary file into text file for each block, which will generate another file called block*.ldm.txt.
Tips for parallel computing: This step can be carried out by computing each chromosome or block separately. To compute chromosomes in parallel using array job submittion (i is the job index), you can do
gctb --bfile ldRef.chr$i --make-block-ldm --block-info ref4cM_v37.pos --out ldm --thread 4
where ldRef.chr$i is the bed file that only contains data for the ith chromosome (while the ldBlockInfo file ref4cM_v37.pos is still genome-wide). To compute all blocks in parallel, you can do
gctb --bfile ldRef --make-block-ldm --block $i --block-info ref4cM_v37.pos --out ldm
where ldRef needs to be the genome-wide bed file. Here using a single thread is sufficient.
After all chromosomes/blocks are done, run the command below to merge info files across blocks. Do not need to run this if you are NOT doing chromosomes/blocks separately.
gctb --ldm ldm --merge-block-ldm-info --out ldm
Step 2: perform eigen-decomposition in each block
Skip this step if you are using the eigen-decomposition data provided by us. The command below will perform eigen-decomposition for each block one by one and store the result in binary format block*.eigen.bin in folder ldm. Again, you can check the file content with --write-ldm-txt which will produce a text file.
gctb --ldm ldm --make-ldm-eigen --out ldm --thread 4
Tips for parallel computing: This step can also be done for each block in parallel by using array job submittion:
gctb --ldm ldm --make-ldm-eigen --block $i --out ldm
No merging is needed after completing all blocks.
Genome-wide Fine-mapping analysis
The Genome-wide Bayesian Mixture Model (GBMM) implemented in GCTB (e.g., SBayesRC) can perform genome-wide fine-mapping analysis. These methods require summary-level data from genome-wide association studies (GWAS) and linkage disequilibrium (LD) data from a reference sample. Our manuscript is currently under review and available at here (link to manuscript).
We outline below on how to perform the genome-wide fine-mapping analysis and calculate the credible set using GCTB.
Run genome-wide fine-mapping analysis
gctb --sbayes RC --ldm-eigen ldm --gwas-summary test.ma --annot annot.txt --n-dist-auto --write-mcmc-bin --out test --thread 4
--sbayes specifies the method to perform genome-wide fine-mapping analysis, e.g., RC.
--ldm-eigen specifies a folder containing the eigen-decomposition LD reference data for each block.
--gwas-summary reads summary-level data from GWAS.
--annot reads the annotation file.
--n-dist-auto allows SBayesRC or SBayesR to automatically choose the number of mixture components.
--write-mcmc-bin outputs the MCMC samples in binary format, required output to compute credible sets.
--out saves the genome-wide fine-mapping results for each SNP in .snpRes file and estimates of genetic architecture in .parRes file.
--thread specifies the number of threads to use.
Detailed instructions on generating the eigen-decomposition-based LD reference, on format of GWAS summary data and annotation file can be found at Download.
Calculate credible sets
gctb --cs –-ld-file ldfile –-pip 0.9 –-mcmc-samples test --out test
--cs turns on the flag to calculate credible sets.
--pip specifies the threshold for the coverage of the credible set.
--mcmc-samples reads the MCMC samples output from the genome-wide fine-mapping analysis (see instructions above).
--out saves the full local credible set results in .lcs and summary of local credible set result in .lcsRes. Saves the full global credible set results in .gcs and summary of global credible set result in .gcsRes.
--ld-file reads the LD file containing pairwise LD \$r^2\$ > 0.5 between SNPs.
The required LD file with pairwise LD \$r^2\$ > 0.5 in each LD block can be computed using GCTB and eigen-decomposition LD reference with command line below,
gctb –-get-ld --ld-eigen ldm –-rsq 0.5 --out test --thread 4
--get-ld turns on the flag to compute pairwise LD file using eigen-decomposition based LD reference files.
--ldm-eigen specifies a folder containing the eigen-decomposition LD reference data for each block.
--rsq specifies the \$r^2\$ threshold used to output the pairwise LD result.
--out saves the LD file with pairwise LD \$r^2\$ > 0.5.
FAQ
I obtained a poor prediction accuracy using SBayesR. Why is that and can it be improve?
If the prediction accuracy is unreasonably low using SBayesR, it is likely that a convergence problem has occurred for the trait analysed. Poor convergence will cause the SNP effect sizes to gradually "blow up" (keep increasing toward infinity) and eventually impair prediction accuracy. If you were using GCTB v2.01 or a lower version, you will usually find hsq (i.e., SNP-based heritability) increases to one and SigmaSq (i.e., the variance of SNP effects) keep increasing along with the MCMC iterations, as shown below for example.
Iter NumSnp1 NumSnp2 NumSnp3 NumSnp4 SigmaSq ResVar GenVar hsq Rounding
100 893956 29937 15607 927 0.0003 0.4961 0.5314 0.5172 0.0000
200 915615 23804 3 1005 0.0050 0.0024 0.7879 0.9970 0.0024
300 927659 11282 1 1485 0.0188 0.0000 0.8639 1.0000 0.0017
400 932231 6640 3 1553 0.0551 0.0000 0.9383 1.0000 0.0014
500 934298 4592 16 1521 0.1187 0.0000 1.0284 1.0000 0.0013
600 935284 3699 154 1290 0.2155 0.0000 1.1305 1.0000 0.0015
700 935920 3162 121 1224 0.3423 0.0000 1.2169 1.0000 0.0018
800 936400 2722 148 1157 0.4792 0.0000 1.2991 1.0000 0.0020
900 936671 2431 429 896 0.7588 0.0000 1.3778 1.0000 0.0023
1000 936891 2281 369 886 0.9321 0.0000 1.4472 1.0000 0.0025
At some stage, the program may stop and report the following error message because no SNP can be fitted due to the "blown up".
Error: Zero SNP effect in the model for 100 cycles of sampling
In GCTB v2.02, we flag the convergence issue by the following message when hsq hits 1 (or equivalently, the residual variance < 0):
Error: Residual variance is negative. This may indicate that effect sizes are "blowing up" likely due to a convergence problem. If SigmaSq variable is increasing with MCMC iterations, then this further indicates MCMC may not converge. Please refer to our website (https://cnsgenomics.com/software/gctb) for further information on this problem.
Sometimes, even though the MCMC appears to be completed, the posterior means of SNP effects can still be severely biased due to the convergence problem. It is highly recommeded to visualise the scatter plot of the SBayesR estimated SNP effects versus the GWAS marginal effects if you suspect poor convergence. The figure on the left-hand side shows such a scatter plot when MCMC has converged normally. The figure on the right-hand side shows the case when the convergence problem occurred, where some of the SBayesR effect estimates are orders of magnitude larger than the corresponding GWAS marginal effect estimates.
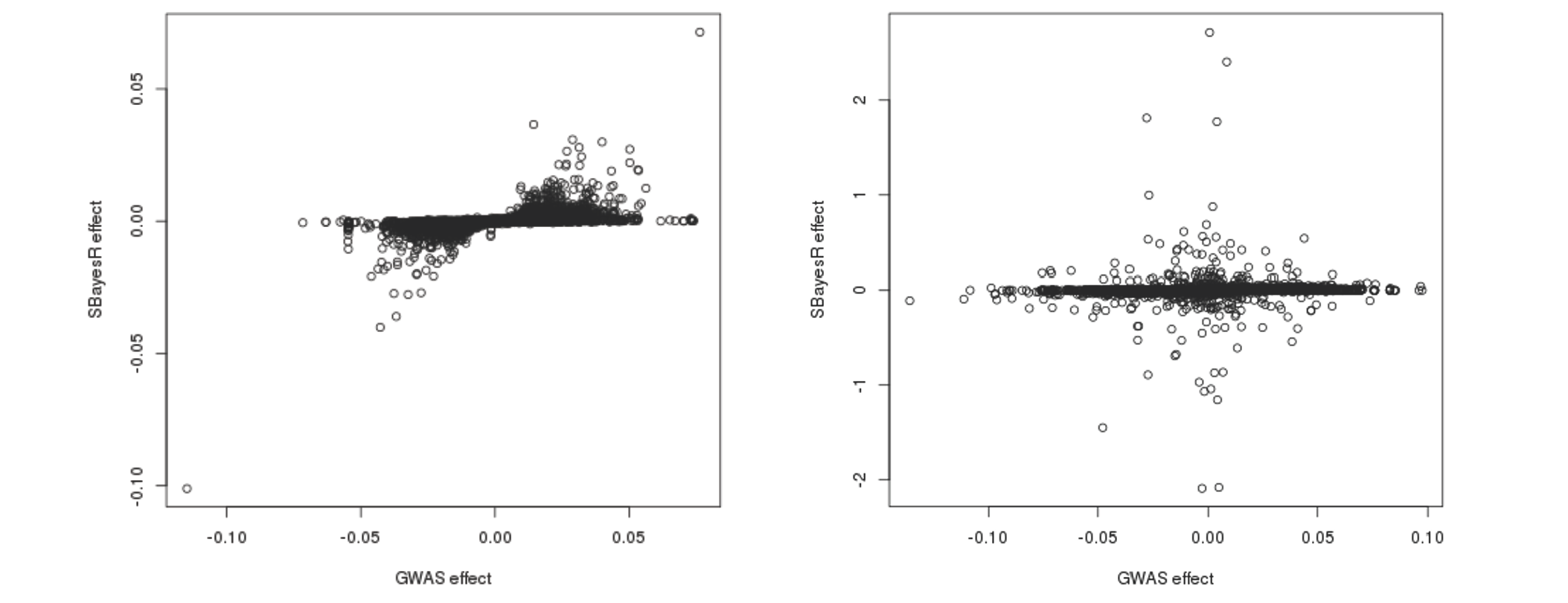
Further plotting the SBayesR effect estimates against the physical positions reveals that some SNPs that are in proximity tend to have their effects "blown up" in opposite directions:
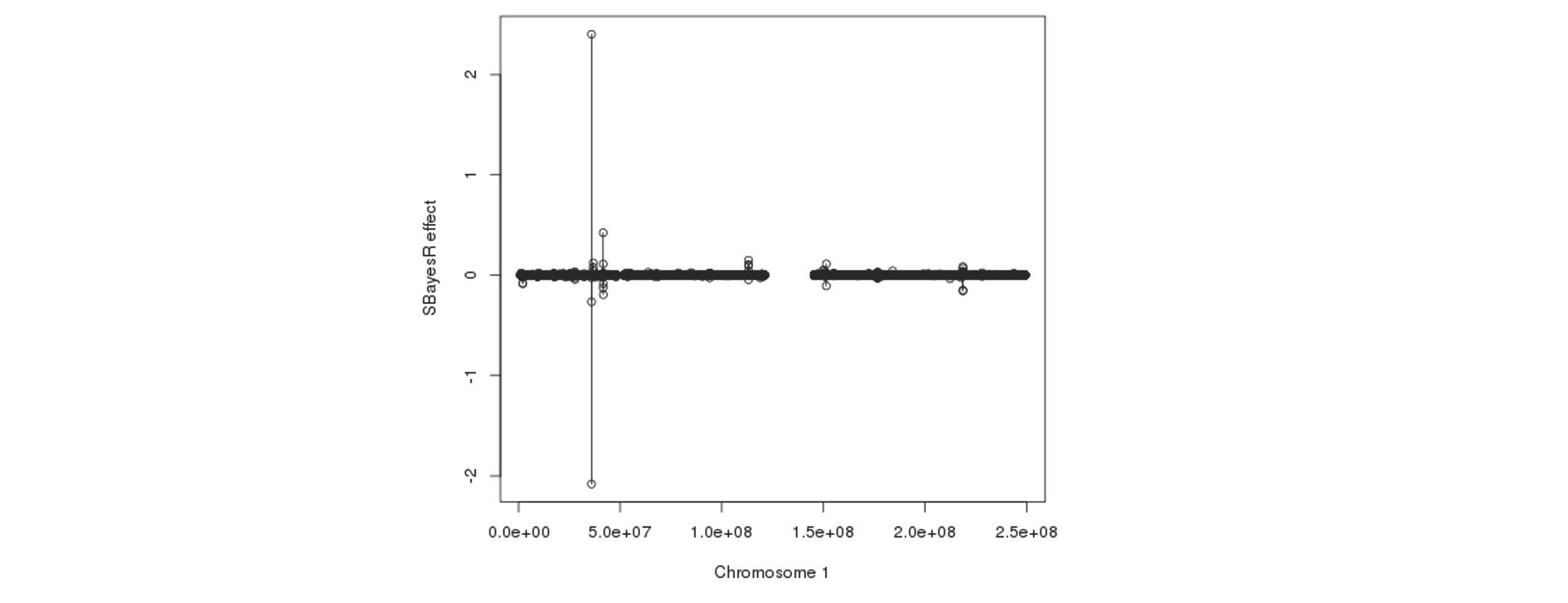
The fundamental cause of the failure in convergence is not exactly clear, but it is most likely because of the inconsistency between the LD reference data and GWAS summary statistics or/and errors in these datasets. We suggest to try the following steps to avoid the convergence problem. Please also see this doc for a detailed description of processing and running of SBayesR for Locke et al. 2015 and Wood et al. 2014.
1. Remove SNPs with extreme GWAS sample sizes.
It is implicitly assumed in SBayesR that all SNPs have the same GWAS sample size; otherwise, the residual covariance stucture is misspecified. This assumption is often violated when some SNPs have large genotype missing rates or when the GWAS summary statistics are from a meta-analysis where not all SNPs are genotyped in all cohorts. Below is an example of a highly skewed distribution of per-SNP sample size from a meta-analysis.
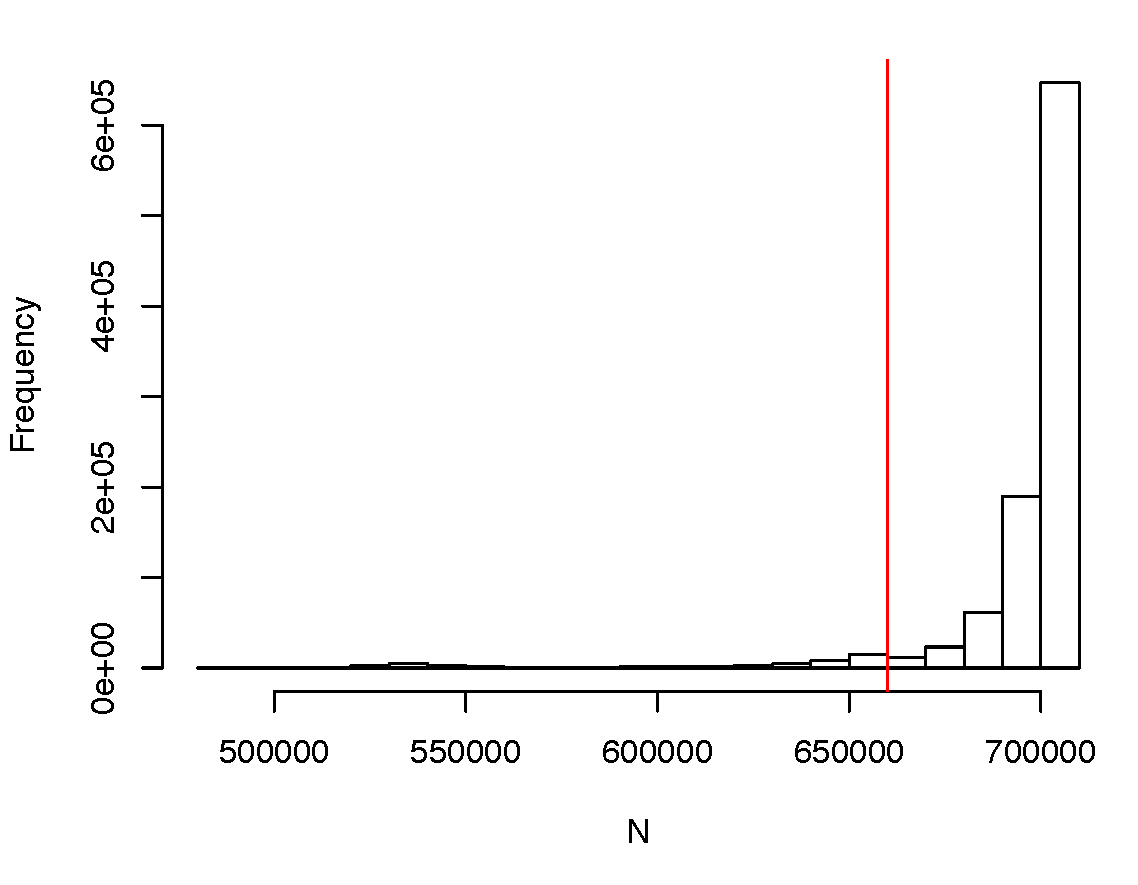
In this case, removing the SNPs in the lowest 10% quantile led to a converged result. It is highly recommended to examine the distribution of per-SNP sample size prior to the analysis and remove the outliers with extreme sample sizes. Sometimes, the average sample size is given for all the SNPs. In such a case, one can use the --impute-n option in GCTB when running SBayesR, which will impute the per-SNP sample size based on the beta values, SE and allele frquenes and exclude SNPs that have the imputed sample sizes 3 standard deviations apart from the median value.
2. Use the shrunk LD matrix.
While in principle any type of LD matrix can be used in SBayesR, using the shurnk LD matrix can lead to the most robust result for some traits, such as height. This is likely because the shrunk LD matrix, which is much less sparse than the sparse LD matrix with the default chi-squared threshold, has a better capacity to capture true LD correlations of very small values. Ignoring the SNPs in small LD correlations with the causal variants can collectively cause a bias in the mean of the full conditional distribution of some SNP effects, and subsequently cause the convergence problem. We have provided two shrunk LD matrices based on a random sample of 50K individuals of European ancestry in UK Biobank data, one with about 1.1 million HapMap3 common SNPs and the other with about 2.8 million common SNPs using a genetic map in the public domain.
3. Use DENTIST to detect and remove SNPs with errors in GWAS or LD reference and heterogeneity between the two.
DENTIST is a software that leverages LD among genetic variants to detect and eliminate errors in GWAS or LD reference and heterogeneity between the two. It could be helpful to run DENTIST prior to SBayesR to identify SNPs that have inconsistent LD properties between GWAS and reference samples, and then use --exclude option in GCTB to exclude those SNPs in the SBayesR analysis.
4. Remove null SNPs based on the GWAS P-values.
It can be seen from the above plot of SBayesR effect against GWAS effect estimates that the "blowing up" occures more frequently to the SNPs with GWAS effects close to zero. We have also observed a significant improvement in SNP-based heritability estimation and prediction accuracy when removing the null SNPs based on the GWAS P-values for some traits. For example, as shown in the figure below, removing SNPs with GWAS P-value greater than 0.4 (or lower) in the Wood et al. (2014 Nat Genet) summary statistics data (after a quality control step on the per-SNP sample size) appeared to fix the convergence problem and led to a substantially improved SNP-based heritability estimates and a higher prediction accuracy. In GCTB, one can use --p-value option to specify the upper bound of the P-values of the SNPs to be included in the analysis.
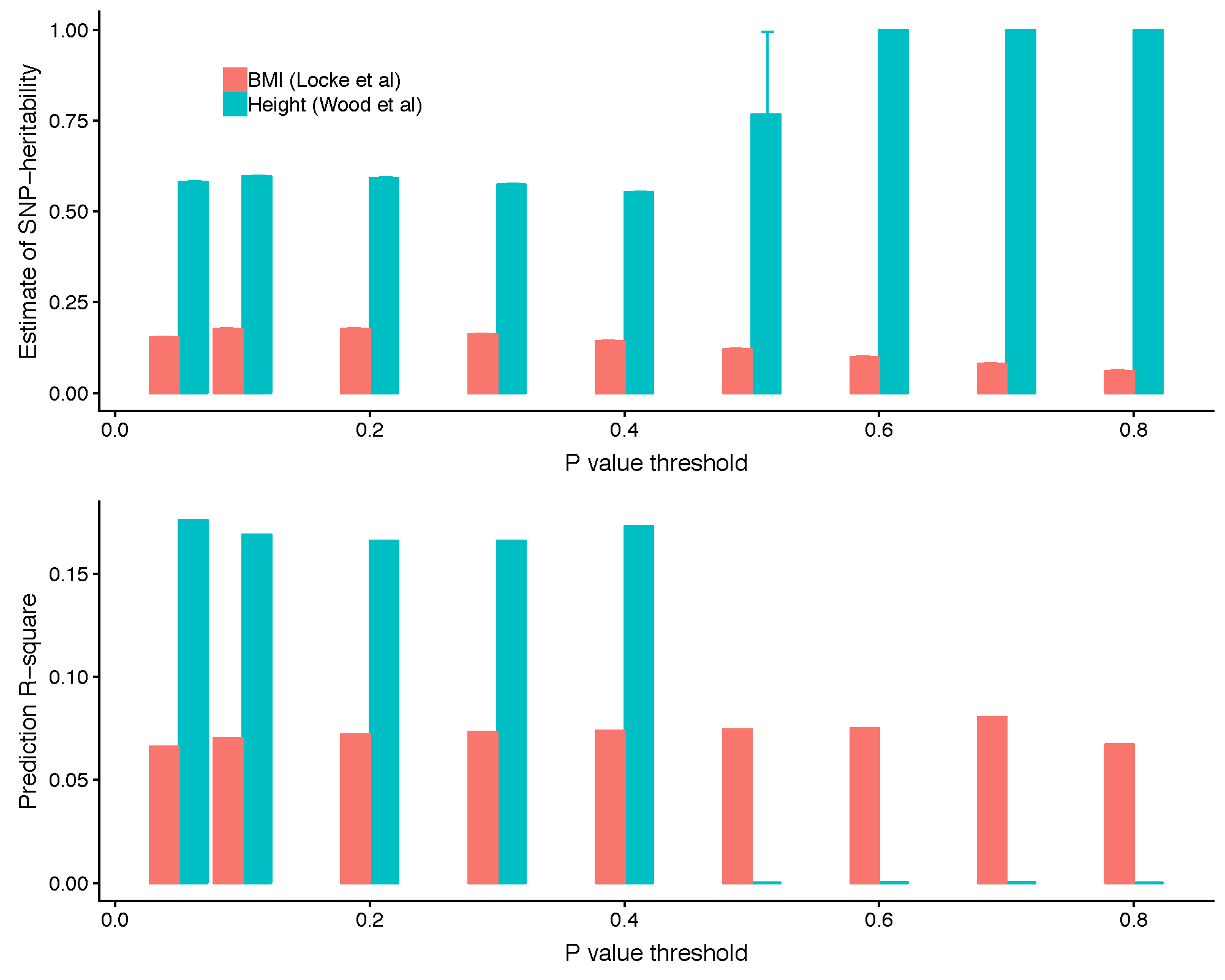
5. Filter SNPs based on the LD R-squared.
When the convergence problem occurred, two SNPs in high LD will sometimes blow up effect sizes in opposite directions, as shown in the figure above. Removing one of the SNPs in high LD could be helpful to mitigate the problem. We have implemented --rsq option in GCTB to detect every pair of SNPs with LD R-square greater than the specified threshold and then remove the SNP with higher GWAS P-value.